藤原さとです。
もう新学期がはじまりましたね。日本に帰国した夏休み。娘の預け先がなかなか見つからず、仕事が全然進まず、半分預かり目的で、受験塾の夏期講習にはじめて通わせてみたのですが、いろいろ面白いことが分かったので書いてみます。
娘は、小学校に入ってからまるまる3年現地校に通い、日本語は土曜日の補習校に通うのみだったので、当然みんなと肩を並べて結果を出してもらいたいというわけではありません。受験目的というよりは日本語に慣れるという特殊な理由で通いました。受講したのは4科目です。
なお、私自身は、中学受験を経験しています。その時は、塾の勉強が大嫌いで、6年生の時には完全にエネルギーが切れ、4科目受験から2科目受験に変更。しかも第1志望も第2志望も落ちてしまい、もはや第3志望なんだか第4希望なのか分からない学校に不本意な気持ちを抱えながら6年間通ったという苦い思い出があります。
今回は、特に面白いな、と思った算数について書きたいと思います。

<教え方次第で面白くなる算数の問題>
初日、二日目と植木算あたりまでは多少混乱しつつもどうにかついてきた娘。しかし等差数列や平面図形の角度の問題になったら、何がなんだか分からなくなってしまったらしく、「算数なんかもう大嫌いだ!」と涙目で帰ってきました。もともと学校の算数は好きで、自信もある娘。これはまずいまずい。
そこで、一緒に問題を解くことにしてみました。私の受験した40年近く前と問題がほとんど変わらないんですね。
でも、あの時あれほど嫌だった等差数列や平面図の問題。改めて見てみたら、非常に面白いのです!なぜかというと、解き方が複数ある問題で、考える余地が多い。また扱っている内容も数学・科学の本質ではありませんか。等差数列の問題は散らばっている数字から何等かの規則や法則を見出し、それを数式化するという非常に大事な作業のまさに入り口。
平面図形の問題も現代数学や理論物理の世界で重要な「対称性」の概念を扱い、複数の角度から図形について考察できるので非常にエキサイティングです。ではなんで、こんな面白い問題を娘(と過去の私)は「つまらない」と認識してしまったのでしょう。
<複数の解き方を考えることからスタートしよう~等差数列>
たとえば、非常に単純な等差数列の問題です。下記の図を参考に20番目の奇数を考えましょう。

こうした時に、塾の教材ではいきなり、奇数の10番目は、1+2×(10-1)=19なので、その式の意味を考えて求めよう、と書いてありました。
でも、解き方はそれだけではありません。なので、娘には上記の数式は一旦忘れて、数字とにらめっこして、自分でなんらかの法則が見つからないかをまず考えてその法則を教えて欲しいと言いました。
そうしたらしばらく考えた後に、まず出してきた解法はこのようなものでした。
「「番号」-1+「番号」で奇数の数字が出るよ!たとえば、番号が9でしょ、それから1を引くと8、8+9=17でこたえがでるよ。なので、20番目なら、20-1+20=39。」
確かにそうです。交差が変化した時に応用が利かないやり方ですので、塾では絶対教えない方法だとは思いますが(笑)正解です。一つ法則を見つけました。
もう一つ解き方を考えてみない?と言うと、嬉々として取り組み始めました。次の解法はこのようなものでした。
「分かった!交差の2を求めたい番号とかけるでしょ、それから1を引くと数字が合うよ。20番目なら、20×2-1=39。」
こちらも正解です。でも塾のやり方ではありません。
さて、最後にやっと塾で指定された計算方法、(20-1)×2+1=39を出してきました。しかし、テキストに載っている1+2(20-1)の順番と頭で考えた数式の順番が違うところがポイントです。
こうしてちょっとだけ工夫をするだけで、本当に楽しそうに子どもは問題に取り組むものです。
<原理を理解して自分で答を見出すプロセス~平面図形>
次の問題は、xの角度を出す問題です。こちらも非常にシンプルですが、いろいろな解き方ができます。
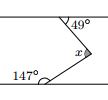
この解き方も、塾では下図のようにxの角のところに定規をあてて真ん中に平行線を描き、解いていくやり方、180-147+49=82°と解くように教えてもらったようです。
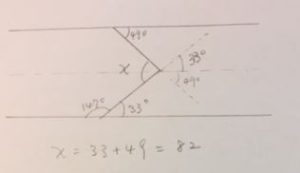
しかし、平行な横線を斜めに横切る直線が交わって横切る角が同じということにピンときていませんでした。
なので、紙とハサミを持ってきて、ありったけの平行線と斜め線、三角形や四角形を自由につくり、三角形の内角の和が180°になること、平行線を斜めに切ると、一緒の角度ができることを何度も何度もやりました。チョキチョキチョキチョキ・・・・
その後、もう一度上記の問題を解くときに一旦塾のやり方を忘れて、自分で図形とにらめっこして、解き方を考えてみて、と言ったら彼女は塾で教えてもらうようなやり方はせず、平行線を書かずに補助線をひいて、三角形の内角の和をつかって別のやり方で問題を解きました。
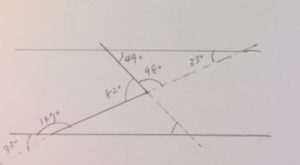
<解き方を工夫すれば受験算数も楽しい>
こうやって、取り組み方を変えると非常に面白い受験算数。今回いきなり夏期講習だったので、もしかしたら学期中に上記のようないろいろな解き方をやってみていたのかもしれませんが、せっかくだったら、解き方を指定するのではなくて、自分(グループ)で解き方を考えていけば、数学的思考もつくし、もっと楽しいと思います。「にらめっこ」がポイントです。
せっかく中学受験をするのであれば、しっかり楽しんでクリエイティブに過ごしたほうが良いだろうと思います。なお、探究学習をするのに、私が言うのもなんですが、いわゆる探究型プログラムを受ける必要があるかといえば、そんなこともないと思います。こうした身近な問題からも自ら仮説を立てて、自分なりの解き方を見出していくような学びは「探究する学び」と言ってよいと思います。
私自身は中学受験には賛成でも反対でもないのですが、受験でもゲームでも、ダンスでも遊びでも夢中になって取り組めるようなら、プラスだと思います。逆もしかりですね。
今のところ、私の娘は受験塾にお世話になる可能性は低そうです(;^_^A が、こんなことを思ったので書きました。
ということで今日はこの辺で。
<私たちについて>
こたえのない学校HP
こたえのない学校ブログ
※こたえのない学校の主催する教育者向け年間プログラムです。
Facebook ページ
https://www.facebook.com/kotaenonai.org

